前言
理解和记住一些常见的模型,解决排列组合问题基本就够用了。
一、排列组合
- 排列、排列数
\(A_n^m=n\times (n-1)\times (n-2)\times\cdots\times (n-m+1)=\cfrac{n!}{(n-m)!}\);\(A_n^n=n!\);\(0!=1\)
引例\(n\in N\),且\(n<55\),则乘积\((55-n)(56-n)\cdots (69-n)\)等于【】
分析:\(69-n\)最大,因式个数为\((69-n)-(55-n)+1=15\),故选\(B\)。
- 组合、组合数
\(C_n^m=\cfrac{A_n^m}{A_m^m}=\cfrac{n\times (n-1)\times (n-2)\times\cdots\times (n-m+1)}{m!}=\cfrac{n!}{m!\cdot (n-m)!}\)
- 排列组合的识别:
若与顺序(次序、位置)有关,则为排列,若与顺序(次序、位置)无关,则为组合。
引例,比如5个人之间彼此留言,则是排列,共有\(A_5^2=20\)种,比如5个人之间彼此握手,则是组合,共有\(C_5^2=10\)种;
二、理解模型
Ⅰ小球放入盒子
①3个不同的小球,放入5个不同的盒子中,每个盒子至多有一个球,共有\(A_5^3\)种不同的放法。
分析:等同于3封信,投入5个不同的邮箱,每个信箱至多一个;或者3个人坐5个凳子。
②3个不同的小球,放入5个不同的盒子中,每个盒子能放入的小球不限,共有\(5^3\)种不同的放法。分析:等同于映射个数问题。
③集合\(A=\{1,2,3\}\),集合\(B=\{a,b,c,d\}\) ,则映射\(f:A \rightarrow B\)的个数为\(4^3\);映射\(f:B \rightarrow A\)的个数为\(3^4\);
④集合\(A=\{1,2,3\}\),集合\(B=\{a,b,c\}\) ,则一一映射\(f:A \rightarrow B\)的个数为\(A_3^3=6\)个,一一映射\(f:B \rightarrow A\)的个数也为\(A_3^3=6\)个。
⑤6个相同的小球,放入3个不同的盒子中,每个盒子至少有一个球,共有\(C_5^2\)种不同的放法。
分析:隔板法,如图所示,\(0\underline{|}0\underline{|}0\underline{|}0\underline{|}0\underline{|}0\),
所求的不同放法个数,相当于在5个空位上插入2个隔板的不同插入方法,共有\(C_5^2=10\)种;
或解:相当于从5个插好的隔板中任意取出三个隔板的不同取出方法,共有\(C_5^3=10\)种;
Ⅱ排队照相
已知有5个同学排队照相,求
①甲、乙两个同学必须相邻的排法有多少种?
分析:\(A_4^4\times A_2^2=48\),相邻问题捆绑策略
②甲、乙、丙三个同学互不相邻的排法有多少种?\(A_2^2\times A_3^3=12\),
分析:不相邻问题插空策略
③乙不能站在甲前面,且丙不能站在乙前面的排法有多少种?
【法1】:只能按照“甲乙丙”的次序来排列,
定序问题,\(\cfrac{A_5^5}{A_3^3}=20\),
定序问题除法策略(有部分相同元素的排列问题和定序问题是相同的)
【法2】:先按照甲乙丙的次序排甲乙丙,仅1种,
然后插入剩余两人中的一人有4种,
最后再插入最后一人有5种,故\(N=4\times 5=20\)
【法3】:先按照甲乙丙的次序排甲乙丙,仅1种,然后插入剩余的两人,分类如下:
当两人不相邻,有\(A_4^2=12\)种,
当两人相邻,有\(C_4^1\times A_2^2=8\)种,
故共有\(A_4^2+C_4^1\times A_2^2=20\)种。
④甲不站在中间位置,乙不站在两端两个位置的排法有多少种?
【法1】:以乙的位置分类,
当乙居中时,先排乙有\(A_1^1\)种,再排其余有\(A_4^4\)种,
则有\(A_1^1\times A_4^4=24\),
当乙不居中时,先排乙有\(A_2^1\)种,再排甲\(A_3^1\)种,
再排其余有\(A_3^3\)种,则有\(A_2^1\times A_3^1\times A_3^3=36\),
故共有\(N=24+36=60\)。
【法2】:以甲的位置分类,类比上法思考。
【法3】:间接法,先5个人做全排列,有\(A_5^5\)种,
然后剔除不符合题意的情形,有甲在中间\(A_4^4\)种或乙在两端\(2A_4^4\)种,
不过这个剔除过程多剔除了甲在中间且已在两端的情形有\(A_1^1(甲)A_2^1(乙)A_3^3\),
故共有 \(A_5^5-A_4^4-2A_4^4+2A_3^3=60\)
⑤排成两排,前排2人,后排3人,有多少种不同的排法?
分析:\(A_5^5=120\)。两排问题拉成一排策略
⑥5个人排成一排,有多少种不同的排法?
分析:\(A_5^5=120\)。
【对照】5个相同的乒乓球排成一排,有多少种不同的排法?
分析:\(C_5^5=1\),或者理解为\(\cfrac{A_5^5}{A_5^5}=1\),5个相同理解为定序问题。
⑦5本书中有三本一样的书,排成一排,有多少种不同的排法?
分析:\(\cfrac{A_5^5}{A_3^3}=20\),3本相同理解为定序问题。
⑧单词“error”的所有拼写形式有多少种?
分析:同上述⑦问题,\(\cfrac{A_5^5}{A_3^3}=20\)。
⑨定序问题,比如【简单的定序】,
4个人按照甲在前,乙在后的确定次序排队,共有多少种不同的排法?
分析:4个人排队,共有\(A_4^4\)种,其中按照甲乙来看,共有\(A_2^2\)类,分为甲前乙后的一类,和甲后乙前的另一类,设每一类有\(x\)种,则\(x\cdot A_2^2=A_4^4\),故\(x=\cfrac{A_4^4}{A_2^2}=12\)种;
提升:6个人按照甲乙丙的确定次序排队,共有多少种不同的排法?
分析:6个人排队,共有\(A_6^6\)种,其中按照甲乙丙来看,共有\(A_3^3\)类,其中甲乙丙的次序只占\(\cfrac{1}{A_3^3}\),设每一类有\(x\)种,则\(x\cdot A_3^3=A_6^6\),故\(x=\cfrac{A_6^6}{A_3^3}\)种;
再提升:\(n\)个玩具排成一排,其中有\(m\)个相同,则共有排法\(\cfrac{A_n^n}{A_m^m}\)种;
Ⅲ分组和分配
按照下列要求分配6本不同的书,各有多少种不同的分配方式?
⑴分成三份(堆),1份1本,1份2本,1份3本 ;
分析:无序不均匀分组问题,\(C_6^1\times C_5^2\times C_3^3=60\);
或者相当于先从6本中任取1本\(C_6^1\)种放成一堆,再从剩余的5本中任取1本\(C_5^2\)种放成一堆,再从剩余的3本中任取3本\(C_3^3\)种放成一堆,到此分成了符合要求的三份,事件完成,故有\(C_6^1\times C_5^2\times C_3^3=60\);
⑵甲、乙、丙三人中,一人得1本,一人得2本,一人得3本
分析:有序不均匀分组问题,先分组再分配到人手中。
\(C_6^1\times C_5^2\times C_3^3\times A_3^3=360\)
⑶平均分成三份,每份2本
分析:无序均匀分组问题,\(\cfrac{C_6^2\times C_4^2\times C_2^2}{A_3^3}=15\)
【解释】先分为三份,则应该是\(C_6^2\times C_4^2\times C_2^2\)种方法;
但是这里出现了重复。不妨记6本书为\(A、B、C、D、E、F\),
若第一步取了\(AB\),若第二步取了\(CD\),若第三步取了\(EF\),标记该种分法为\((AB,CD,EF)\),
则\(C_6^2\times C_4^2\times C_2^2\)种方法中还有\((AB,EF,CD)\),\((CD,AB,EF)\),\((CD,EF,AB)\),
\((EF,AB,CD)\),\((EF,CD,AB)\),共有\(A_3^3\)种情况,
而这\(A_3^3\)种情况仅仅是\(AB、CD、EF\)的顺序不同,因此只能作为一种分法,
故分配分法有\(\cfrac{C_6^2\times C_4^2\times C_2^2}{A_3^3}=15\)种。可以类比定序问题理解。
⑷平均分配给甲、乙、丙三人,每人2本
分析:有序均匀分组再分配问题,\(\cfrac{C_6^2\times C_4^2\times C_2^2}{A_3^3}\times A_3^3=90\)
或解:先让甲来领取有\(C_6^2\)种,再让乙来领取有\(C_4^2\)种,最后让丙来领取有\(C_2^2\)种,
故有\(C_6^2\times C_4^2\times C_2^2=90\)
⑸分成三份,1份4本,另外两份每份1本
分析:无序部分均匀分组,\(\cfrac{C_6^4\times C_2^1\times C_1^1}{A_2^2}=15\),
其中每份1本的这两堆是大小一样,没有顺序的,故需要除以\(A_2^2\)。
⑹甲、乙、丙三人中,一人得4本,另外两人每人得1本
分析:有序部分均匀分组再分配问题,\(\cfrac{C_6^4\times C_2^1\times C_1^1}{A_2^2}\times A_3^3=90\)
⑺甲得1本,乙得1本,丙得4本
分析:直接分配问题,\(C_6^1\times C_5^1\times C_4^4=30\)
或者\(C_6^4\times C_2^1\times C_1^1=30\)
备注:其中第⑺问,相当于甲乙丙这三个人依次上来领取一样,
这样的话,“领取”模型就可以同化第⑴、⑷问了。
Ⅳ先分组再分配
①3个不同的小球分给3个人,每个人至少有一个球的不同分法?
分析:共有\(\cfrac{C_3^1C_2^1C_1^1}{A_3^3}\cdot A_3^3=C_3^1C_2^1C_1^1\),或者\(A_3^3\)种不同的放法。
评:整体平均分组。
②4个不同的小球分给3个人,每个人至少有一个球的不同分法?
分析:共有\(\cfrac{C_4^2C_2^1C_1^1}{A_2^2}\cdot A_3^3=C_4^2A_3^3\)种不同的放法。
评:部分平均分组。
③5个不同的小球分给3个人,每个人至少有一个球的不同分法?
分析:共有\(\cfrac{C_5^3C_2^1C_1^1}{A_2^2}\cdot A_3^3+\cfrac{C_5^2C_3^2C_1^1}{A_2^2}\cdot A_3^3\)种不同的放法。
评:分类讨论+部分平均分组。
三、廓清关系
- 计数原理和排列组合的关系
计数原理统管排列组合,排列组合简化计数原理的步骤。
如5人排成一排,应该用乘法计数原理,\(\Delta\;\;\Delta\;\;\Delta\;\;\Delta\;\;\Delta\)
位置1有5种(或\(C_5^1\)),位置2有4种(或\(C_4^1\)),位置3有3种(或\(C_3^1\)),
位置4有2种(或\(C_2^1\)),位置5有1种(或\(C_1^1\));
故共有不同的排列方法\(N=5\times 4\times 3\times 2\times 1=120\)种,
或\(N=C_5^1 \times C_4^1 \times C_3^1 \times C_2^1 \times C_1^1=120\)种,
但如果有了排列的模型,就可以简化为\(N=A_5^5=120\)种。
四、典例剖析
在排列组合题目中,有时候找出错误比换个思路解题更难,所以一旦发现错误,以后就一定要注意避免按照那种模式思维,另外熟练掌握上述的模型,在具体题目的求解中,我们只要能将题目顺利转化为模型就可以求解了。
例15个男生4个女生组成一个4人小组,要求小组中至少要有一男生一女生,有多少种分法?
法1(直接法):分类计数,有一男三女,两男两女,三男一女三种情况,故有:\(C_5^1C_4^3+C_5^2C_4^2+C_5^3C_4^1=120\)
法2(学生容易这样思考的保底法):\(C_5^1C_4^1C_7^2=420\) ,明显法2是有重复的,
比如5个男生为 \(A、B、C、D、E\) ,4个女生为甲、乙、丙、丁;
那么取出的(\(B\),乙,\(A\)甲)和(\(A\),甲,\(B\)乙)、(\(A\),乙,\(B\)甲)等等是一回事,
也就是说这种思路的计数是有重复的,所以要避免这样思考。
反思总结:凡是题目中出现至少至多这样的关键词,则往往需要分类计数或用间接法思考,如果用保底法就会出错。
法3(间接法):\(C_9^4-C_5^4-C_4^4=120\)。
例2【2017全国卷2理科第6题高考真题】
安排3名志愿者完成4项工作,每人至少完成1项,每项工作由一个人完成,则不同的安排方式共有【】种。
分析:部分平均分组再分配问题,
可以先将4项工作分成3份\((1个+2个+1个)\)的情形,共有\(\cfrac{C_4^2C_2^1C_1^1}{A_2^2}\)种,
然后将分成的3组工作分配给3个人,有\(A_3^3\)种,故有\(\cfrac{C_4^2C_2^1C_1^1}{A_2^2}\cdot A_3^3=36\)种。
引申-1:安排3名志愿者完成5项工作,每人至少完成1项,每项工作由一个人完成,则不同的安排方式共有多少种?
安排5名毕业生到3个单位实习,则每个单位至少去一名的不同分派方法有多少种?
分析:将工作分配给人:\(\cfrac{C_5^3C_2^1C_1^1}{A_2^2}\cdot A_3^3+\cfrac{C_5^2C_3^2C_1^1}{A_2^2}\cdot A_3^3=150\);
引申-2:将5名志愿者分配到3个单位,每个单位至少分配1人,则不同的安排方式共有多少种?
分析:将人分到单位:\(\cfrac{C_5^3C_2^1C_1^1}{A_2^2}\cdot A_3^3+\cfrac{C_5^2C_3^2C_1^1}{A_2^2}\cdot A_3^3=150\);
引申-3:将5名志愿者分配到3个单位,每个单位至少分配1人,其中甲同学不能分配到\(A\)宿舍,则不同的安排方式共有多少种?
分析:不考虑甲同学的情形,共有\(\cfrac{C_5^3C_2^1C_1^1}{A_2^2}\cdot A_3^3+\cfrac{C_5^2C_3^2C_1^1}{A_2^2}\cdot A_3^3=150\)种;
其中将甲分配到\(A\)宿舍占总数的\(\cfrac{1}{3}\),故甲同学不能分配到\(A\)宿舍的不同方式有\(150\times (1-\cfrac{1}{3})=100\)。
引申-4在送医下乡活动中,某医院安排甲、乙、丙、丁、戊五名医生到三所乡村医院工作,每所医院至少安排一名医生,且甲、乙两人不能安排在同一个医院,丙、丁两人也不能安排在同一个医院,则不同的分配方法种数为__________。
分析:将五人安排到三所医院,且每所医院至少安排一名医生,则不同的分组方式有\(1+1+3\)和\(1+2+2\)两种,
当分组方式为\(1+2+2\)时,用间接法求解,所有的分配方法共有\(\cfrac{C_5^3C_2^1C_1^1}{A_2^2}\cdot A_3^3\)种,其中不符合题意的有甲乙两人同医院的,\(C_2^2(选甲乙)C_3^2(另三人选一个)C_1^1(剩余一人)A_3^3\),丙丁两人同医院的,\(C_2^2(选丙丁)C_3^2(另三人选一个)C_1^1(剩余一人)A_3^3\),在这其中多算了甲乙同医院且丙丁同医院的情形\(A_3^3\),故共有\(\cfrac{C_5^3C_2^1C_1^1}{A_2^2}\cdot A_3^3-(2C_3^2A_3^3-A_3^3)=90-30=60\);
当分组方式为\(1+1+3\)时,用直接法求解,从甲乙两人中选一个\(C_2^1\),从丙丁两人中选一个\(C_2^1\),将剩余的三人自然合成一组共三组,再分配有\(A_3^3\),故共有\(C_2^1C_2^1A_3^3=24\);
综上所述,共有\(N=60+24=84\)种。
例3【北师大选修2-3\(P_{17}B\).02】某校乒乓球队有男运动员10名和女运动员9名,若要选出男女运动员各3名参加混合双打比赛(每名运动员只限参加一场比赛),共有多少种比赛方法?
分析:\(C_{10}^3\cdot C_9^3\cdot A_3^3\),其中男女各3人的混合双打有\(A_3^3\)种。
例4如图所示,使电路接通,开关不同的开闭方式共有【】种。

法1:第一组开关中至少有一个接通有\(2^2-1=3\)种,第二组开关中至少有一个接通有\(2^3-1=7\)种,由乘法原理可知\(3\times7=21\),故选\(D\)。
法2:\((C_2^1+C_2^2)(C_3^1+C_3^2+C_3^3)=21\),故选\(D\)。
例5从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有一名女生,共有【】种不同的选法。
分析:先选出4个人,有“一女三男”和“二女二男”两种情况,\(C_2^1\cdot C_6^3+C_2^2\cdot C_6^2\)
然后在这4个人中,再安排队长和副队长\(A_4^2\)。
共有\((C_2^1\cdot C_6^3+C_2^2\cdot C_6^2)\cdot A_4^2=660\)种。
例6【选修2-3,P22 A组第4题】从\(1\),\(2\),\(3\),\(4\),\(7\),\(9\)中任取不相同的两个数,分别作为对数的底数和真数,能得到多少个对数值?
法1:直接法,分类计数,
第一类,底数和真数中不含\(1\),共有\(A_5^2=20\)种,再减去4种重复的情况(\(log_23=log_49\);\(log_32=log_94\);\(log_24=log_39\);\(log_42=log_93\)),有\(16\)种;
第二类,真数中含有\(1\),即\(log_21=log_31=log_41=log_71=log_91=0\),只有1种;
综上所述,共有\(16+1=17\)个不同的对数值。
法2:间接法,从\(6\)个数字中任选一个做底数(不能为1)有\(C_5^1\)种,然后在剩余的5个数字中任选一个做真数有\(C_5^1\)种,
故不计特殊情况共有\(C_5^1\times C_5^1=25\)种,其中需要剔除的有类似\(log_a1=0\)的有\(4\)种,
以及这样的\(4\)种(\(log_23=log_49\);\(log_32=log_94\);\(log_24=log_39\);\(log_42=log_93\)),
综上所述,共有\(25-4-4=17\)个不同的对数值。
例8\(a,b,c,d,e\)共5个人,从中选1名组长1名副组长,但\(a\)不能当副组长,不同的选法种数为【】
分析:由于选出的人中,可能有\(a\),也可能没有\(a\),故需要分类讨论:
当选出的人中没有\(a\)时,有\(C_4^2\cdot A_2^2=12\);
当选出的人中有\(a\)时,则\(A_1^1\cdot A_4^1=4\);
故不同的选法共有\(12+4=16\)。故选\(B\)。
例9从6名志愿者中选出4人,分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两人不能从事翻译工作,则选派方案共有【】种。
分析:由于选出的人中,可能有甲、乙两个人,也可能都没有,也可能只有一个人,故需要分类讨论:
当选出的人中不包含甲、乙两人时,有\(A_4^4=24\)种;
当选出的人中只包含甲、乙两人中的一人时,先选后排,有\(C_2^1\cdot C_4^3\cdot A_3^1\cdot A_3^3=144\)种;
当选出的人中包含甲、乙两人时,先选后排,有\(C_2^2\cdot C_4^2\cdot A_3^2\cdot A_2^2=72\)种;
故共有\(N=240\)种。
例10某班举行晚会,原定的五个节目已排出节目单,演出前又增加了两个节目,若将这两个节目插入原节目单中,则不同的插法总数为【】
分析:按照这两个节目是否相邻分类讨论如下:
当插入的两个节目相邻,则有\(C_6^1\cdot A_2^2=12\)种;
但插入的两个节目不相邻,则有\(A_6^2=30\)种;
故共有\(N=12+30=42\)种。故选\(A\)。
例11某城市的街道如图所示,某人要从\(A\)地到\(B\)地,则路程最短的走法共有【】种
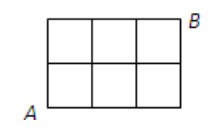
法1:列举法,依次画出,共有10种,故选\(B\)。
法2:组合法,类似于二项展开式的项的构成一样,从\(A\)地到\(B\)地的走法,必须且只需向上或向右,分析可知,需要向上两次,向右三次,相当于从\((a+b)^5\)种选3个\(a\),选2个\(b\),故选法为\(C_5^3\cdot C_2^2=10\)种,或者\(C_5^2\cdot C_3^3=10\)种,故选\(B\)。
例12从6个正方体拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为【】
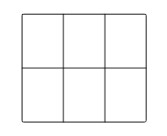
分析:间接法,从12个顶点中任取3个共有\(C_{12}^3\)个,然后排除不符合题意的三种情形:
其一,三个顶点在同一行的有\(3\cdot C_4^3=12\)种;
其二,三个顶点在同一列的有\(4\cdot C_3^3=4\)种;
其三,三个顶点位于田字格的对角线上的有4种,
故共有\(N=C_{12}^3-12-4-4=200\)种,故选\(C\)。
例13设\(\{a_n\}\)为等差数列,从\(\{a_1,a_2,a_3,a_4,a_5,a_6,a_7,a_8,a_9,a_{10}\}\)中任取4个不同的数,使这3个数仍成等差数列,则这样的数列最多有_________个。
分析:按照取出的三个数相隔的项数分类讨论如下:
其一,取出的四个数相连的有7个,其逆序也成等差数列,故共有\(7\times2=14\)个;比如\(\{a_1,a_2,a_3,a_4\}\),\(\{a_2,a_3,a_4,a_5\}\),\(\cdots\),\(\{a_7,a_8,a_9,a_{10}\}\);
其二,取出的四个数隔了一项的,有4个,其逆序也成等差数列,故共有\(4\times2=8\)个;\(\{a_1,a_3,a_5,a_7\}\),\(\{a_2,a_4,a_6,a_8\}\),\(\{a_3,a_5,a_7,a_9\}\),\(\{a_4,a_6,a_8,a_{10}\}\),
其三,取出的四个数隔了两项的,有1个,其逆序也成等差数列,故共有\(1\times2=2\)个;
故共有\(N=14+8+2=24\)个。
例14【2018江西南昌二模】在《周易》中,长横表示阳爻,两个短横表示阴爻.有放回地取阳爻和阴爻三次合成一卦,共有\(2^3=8\)种组合方法,这便是《系辞传》所说“太极生两仪,两仪生四象,四象生八卦”.有放回地取阳爻和阴爻一次有2种不同的情况,有放回地取阳爻和阴爻两次有4种情况,有放回地取阳爻和阴爻三次,有8种情况.所谓的“算卦”,就是两个八卦的叠合,即共有放回地取阳爻和阴爻六次,得到六爻,然后对应不同的解析.在一次所谓“算卦”中得到六爻,这六爻恰好有三个阳爻、三个阴爻的概率是【】
分析:六爻共有\(2^6=64\)种,其中三阳爻三阴爻有\(C_6^3=20\)种,说明:相当于从\((阳+阴)^6\)展开式中取三阳爻三阴爻,故有\(C_6^3\cdot C_3^3=20\)种,则所求概率为\(P=\cfrac{20}{64}=\cfrac{5}{16}\),故选\(C\)。
例15某学校食堂早餐只有花卷、包子、面条和蛋炒饭四种主食可供食用,有5名同学前去就餐,每人只选择其中一种,且每种主食都至少有一名同学选择.已知包子数量不足,仅够一人食用,甲同学肠胃不好不会选择蛋炒饭,则这5名同学不同的主食选择方案种数为【】
分析:甲相当于特殊元素,包子相当于特殊位置,故针对甲分类讨论如下:
①当甲选取包子时,有1种选法,接下来剩余4个人三种食物,有\(\cfrac{C_4^2C_2^1C_1^1}{A_2^2}\cdot A_3^3=C_4^2A_3^3=36\)种;
②当甲不选包子时,先从另外4人中选出1人吃包子有\(C_4^1=4\)种,然后让甲选食物,在花卷和面条中二选一有2种,接下来剩余的人有3人,但食物有2或3种,故需要再次分类讨论
当剩余3人中有1人选取和甲相同,则有\(C_3^1=3\)种,剩余有\(A_2^2\)种,故有\(C_3^1A_2^2=6\)种;
当剩余3人中没有人选取和甲相同,则三人选两种食物,每种食物必须都有人选,有\(C_3^2A_2^2=6\)种;
故当当甲不选包子时,共有\(4\times 2\times(6+6)=96\)种;
综上共有\(N=36+96=132\)种,故选\(B\)。
例16
五、备忘例题
例1【映射个数和函数个数模型】
给定集合\(A=\{1,2,3\}\),集合\(B=\{a,b,c,d\}\) ,求映射\(f:A \rightarrow B\)的个数和映射\(f:B \rightarrow A\)的个数。
分析:依据映射的概念,映射\(f:A \rightarrow B\)需要给集合\(A\)中的每一个元素(原像),都找一个确定的对应对象(像)。
此时注意,原像必须有与之对应的唯一的像,但是像不一定必须有原像和她对应。
我们分步完成:先给元素\(1\)分配对象,每次取一个有\(a、b、c、d\)四种选择;
再给元素\(2\)分配对象,每次取一个也有\(a、b、c、d\)四种选择;
最后给元素\(3\)分配对象,每次取一个也有\(a、b、c、d\)四种选择,
允许出现元素\(1、2、3\)都对应到元素\(a\)上而其他元素没有原像与之对应的情形出现;
利用乘法原理,映射\(f:A \rightarrow B\)共有\(4\times 4\times4=4^3\)个,即\((cardB)^{cardA}\)个。
同理,映射\(f:B \rightarrow A\)共有\(3^4\)个,即\((cardA)^{cardB}\)个。
【引申】:若集合\(B\)为数集,则能构成的函数\(f:A \rightarrow B\)共有\(4\times 4\times4=4^3\)个,
能构成的函数\(f:B \rightarrow A\)共有\(3^4\)个,若集合\(B\)不为数集,则所求的函数个数都是\(0\)个。
原因是:函数是非空数集到非空数集的映射。
例2【映射个数和函数个数模型】
给定集合\(A=\{1,2,3\}\),集合\(B=\{a,b,c\}\) ,求一一映射\(f:A \rightarrow B\)的个数和一一映射\(f:B \rightarrow A\)的个数。
分析:先分析一一映射\(f:A \rightarrow B\)的个数,由于是一一映射,类似有3人坐3个凳子,故有\(A_3^3=6\)个。
同理,一一映射\(f:B \rightarrow A\)的个数也是\(6\)种。
例3 10个相同的小球,分给3个人,允许有人不取,必须分完,共有多少种不同的取法?
法1:以甲取到的小球的个数分类计数如下,
第一类:甲取0个,乙可以取 0~10个 ,丙对应可以取10~0个,有11种不同的取法;
第二类:甲取1个,乙可以取 0~9个 ,丙对应可以取9~0个,有10种不同的取法;
第三类:甲取2个,乙可以取 0~8个 ,丙对应可以取8~0个,有9种不同的取法;
以此类推,
第十一类:甲取10个,乙可以取 0个 ,丙对应可以取0个,有1种不同的取法;
故共有\(N=1+2+3+\cdots+11=\cfrac{(1+11)\times 11}{2}=66\)
法2:隔板法,为保证每个人都取到球,给每个人都补一个球(虚的),
这样就有13个球,形成了12个空位,
用隔板法有\(C_{12}^2=66\)种。
法3:以瓜分10个小球的人的个数分类计数如下:
第一类:仅仅一个人瓜分了10个球,给甲、乙、丙三人,有3种;
第二类:有两个人瓜分了10个球,\(C_9^1C_3^2=27\),
\(C_9^1\)是隔板法的意思(10个球之间形成9个空位,在任意一个空位上插入一个隔板就可以了),
\(C_3^2\)是从三人中任取两个人。
第三类:有三个人瓜分了10个球,隔板法,\(C_9^2=36\),隔板法
故共有\(N=3+27+36=66\)种。
例420个相同的球分给3个人,要求每人至少分3个,共有多少种分配方法?
法1:第一步,先给每人分给3个球,只有1种方法,此时还有11个球。
第二步,到此问题转化为“把11个相同的小球,分给3个人,允许有人不取,必须分完”,
可以仿上完成,共有\(C_{13}^2=78\)种。
体会数学中的转化划归的思想的重要性。
法2:仿上法1,分类计数,共有\(C_{13}^2=78\)种。




(2017秋•市南区期末)[问题提出]
一个边长为ncm (n≥3)的正方体木块,在它的表面涂上颜色,然后切成边长为1cm的小正方体木块,没有涂上颜色的有多少块?只有一面涂上颜色的有多少块?有两面涂上颜色的有多少块?有三面涂上颜色的多少块? [问题探究] 我们先从特殊的情况入手 (1)当n=3时,如图(1) 没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有1×1×1=1个小正方体; 一面涂色的:在面上,每个面上有1个,共有6个; 两面涂色的:在棱上,每个棱上有1个,共有12个; 三面涂色的:在顶点处,每个顶点处有1个,共有8个.(2)当n=4时,如图(2)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体: 一面涂色的:在面上,每个面上有4个,6个面,共有24个; 两面涂色的:在棱上,每个楼上有2个,共有24个; 三面涂色的:在顶点处,每个顶点处有1个,共有8个. … [问题解决] 一个边长为ncm (n≥3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有 (n﹣2)3 个小正方体;一面涂色的:在面上,共有 6(n﹣2)2 个; 两面涂色的:在棱上,共有 12(n﹣2) 个; 三面涂色的:在顶点处,共 8 个. [问题应用] 一个大的正方体,在它的表面涂上颜色,然后把它切成棱长1cm的小正方体,发现有两面涂色的小正方体有96个,请你求出这个大正方体的体积. [问题拓展] 把一个长16cm、宽10cm、高8cm的长方体表面涂上红漆,然后把它切成棱长2cm的小正方体,没有面涂色有几块,一面涂色有几块,两面涂色有几块,三面涂色有几块?【考点】38:规律型:图形的变化类;I1:认识立体图形.菁优网版权所有
【专题】2A:规律型. 【分析】[问题解决]依据正方体内部的小正方体的体积之和,可得没有涂色的正方体数量;依据正方体每个面上的内部的小正方体的面积,即可得到一面涂色的正方体的数量;依据正方体的棱上处于中间部分的小正方体的数量,可得两面涂色的小正方体数量;依据正方体的顶点数量,即可得到三面涂色的小正方体的数量; [问题应用]设正方体棱长为ncm,依据有两面涂色的小正方体有96个,可得方程12(n﹣2)=96,再根据棱长即可得到体积; [问题拓展]依据一个长16cm、宽10cm、高8cm的长方体表面涂上红漆,把它切成棱长2cm的小正方体,类比上述问题的解决方法,即可得到没有面涂色有几块,一面涂色有几块,两面涂色有几块,三面涂色有几块. 【解答】解:[问题解决] 一个边长为ncm (n≥3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有(n﹣2)3个小正方体;一面涂色的:在面上,共有6(n﹣2)2个; 两面涂色的:在棱上,共有12(n﹣2)个; 三面涂色的:在顶点处,共8个. 故答案为:(n﹣2)3,6(n﹣2)2,12(n﹣2),8; [问题应用] 设正方体棱长为ncm, ∵有两面涂色的小正方体有96个, ∴12(n﹣2)=96, ∴n=10, ∴这个大正方体的体积为1000cm3. [问题拓展] 把一个长16cm、宽10cm、高8cm的长方体表面涂上红漆,把它切成棱长2cm的小正方体, 没有面涂色有(16﹣4)(10﹣4)(8﹣4)÷8=36块, 一面涂色有2[(16﹣4)(8﹣4)÷4+(16﹣4)(10﹣4)÷4+(10﹣4)(8﹣4)÷4]=72块, 两面涂色有4[(16﹣4)÷2+(10﹣4)÷2+(8﹣4)÷2]=44块, 三面涂色有8块. 【点评】本题主要考查了正方体,解决问题的关键是抓住表面涂色的正方体切割小正方体的特点:1面涂色的在面上,2面涂色的在棱长上,3面涂色的在顶点处,没有涂色的在内部,由此即可解决此类问题.